Page 25 - TEME

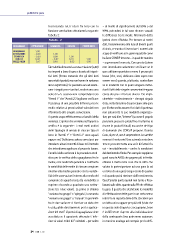
pubbliche gare Incrociando tutti i dati fra loro con la – al livello di significatività del 95% o del funzione correlazione otteniamo la seguente 99%, potendosi in tal caso ritenere casuali Tabella 2: le differenze tra le medie. Altrimenti detta Tabella - 2 ipotesi viene rifiutata. Per tornare ai nostri dati, li esamineremo alla luce di diversi punti MASSIMALE ATTIVAZIONE SCADENZA DURATA PREZZI MEDI di vista, cercando di incrociare i numeri allo MASSIMALE 1,00 ATTIVAZIONE - 0,39 1,00 scopo di verificare se le gare impostate come SCADENZA - 0,30 0,99 1,00 DURATA 0,48 - 0,07 0,10 1,00 hafattoCONSIPriescono–inqualchemaniera PREZZI MEDI - 0,17 0,40 - 0,02 1,00 – a governare il mercato. Con questa dizione Tale tabella dimostra la scarsa relazione (o,48) non intendiamo solamente verificare se le tra importi a base di gara e durata dei rispet- gare abbiano spuntato o meno il prezzo più tivi lotti (fermo restando che gli altri dati basso (che, anzi, abbiamo visto sopra non sono stati riportati, ma non hanno in sostanza essere vero) quanto, piuttosto, controllare alcun significato). Se passiamo ora ad esami- se le modalità con le quali vengono indivi- nare i singoli prezzi unitari, realizziamo una duati i lotti delle singole convenzioni tengono serie di 575 osservazioni comprendenti sia conto dei prezzi fra loro diversi. Ciò impli- “Arredi 1” che “Arredi 2”. Vogliamo verificare cherebbe – evidentemente – che ogni singola l’esistenza di una possibile differenza tra le ditta, nella decisione di partecipare alla gara medie relative ai prezzi unitari calcolati con per il lotto scelto assume fra i dati di partenza riferimento alle singole convenzioni. non solamente le sue modalità organizza- A questo scopo effettueremo un’analisi della tive, per così dire, “interne” (su come il proprio varianza. L’ipotesi che vorremo sottoporre a peculiare processo produttivo trasforma le verifica è la seguente : i costi medi unitari risorse in prodotti finali) ma anche del tipo delle tipologie di arredo di ciascun tipo di di domanda che CONSIP propone. Questo lotto in “Arredi 1” e “Arredi 2” sono uguali fatto,diper sé, nonèsorprendente.Losarebbe oppure no? Dobbiamo adesso arrestarci per semmai il contrario! Una azienda seria deve introdurre alcuni concetti di base ed il metodo tenere presente tutta una serie di fattori fra che intendiamo applicare al presente lavoro. cui – inevitabilmente – anche le condizioni L’analisi della varianza è la procedura stati- del destinatario finale. Per esempio: sappiamo stica per la verifica della uguaglianza fra le quali sono le AASS che pagano più in fretta: medie, ed è realizzata ponendo a confronto ebbene è insito nelle cose che la ditta che la variabilità delle medie di ciascun campione valuta la partecipazione ad una gara (o ad intorno alla media generale con la variabi- un lotto di una gara) tenga conto di quanto lità delle osservazioni intorno alla media del e di quando potrà rientrare dall’investimento. campione di appartenenza (la variabilità si Quest’analisi punta quindi non tanto a foca- esprime elevando a quadrato una sottra- lizzarsisulleditte,quantosullaPAcheeffettua zione tra i due valori). La prima si chiama la gara. È questa che decidendo le modalità “varianza tra gruppi” o “spiegata”, la seconda di effettuazione delle gare in un certo senso “varianza nei gruppi” o “casuale”. Il quoziente indirizza la risposta delle ditte. Decidere per tra le due varianze ci fornisce un dato che un lotto unico oppure per più lotti (visto che è utilizzabile direttamente per la applica- in questa sede di questo ci occupiamo..) non zione del test F. L’ipotesi di uguaglianza viene è indifferente rispetto alla individuazione accettata se il quoziente ottenuto è infe- della controparte (ma potremmo ragionare riore ai valori critici di F calcolati – per solito in maniera analoga ad esempio per la defi- 24 TEME 1.10